Build an Elongated Hexagon Table

Free Furniture Plans to Build a Beautiful Table

Previously, I shared plans for a regular hexagon table. Now, I am sharing free furniture plans to build an Elongated Hexagon Table. This table is perfect for a large, open space and will seat several! It would be a fabulous addition to a large family gathering or dinner party!

Materials:

• 1-1/4″ pocket hole screws
• 1-1/4″ brad nails
• Edge banding, optional (<– affiliate link!)
• Wood glue
• Sandpaper (100, 150, 220 grits)
• Finishing supplies (primer & paint, or stain, sealer)

Lumber:

• 8 – 1×3 at 6′
• 2 – 2×2 at 6′
• 1 sheet of 3/4″ plywood

Cut List:

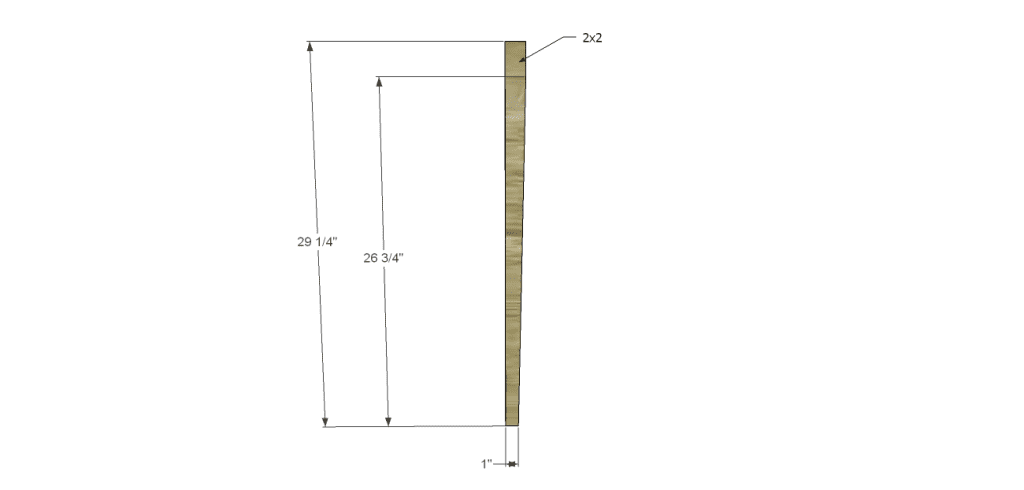
• 6 – 2×2 at 29-1/4″ – Legs
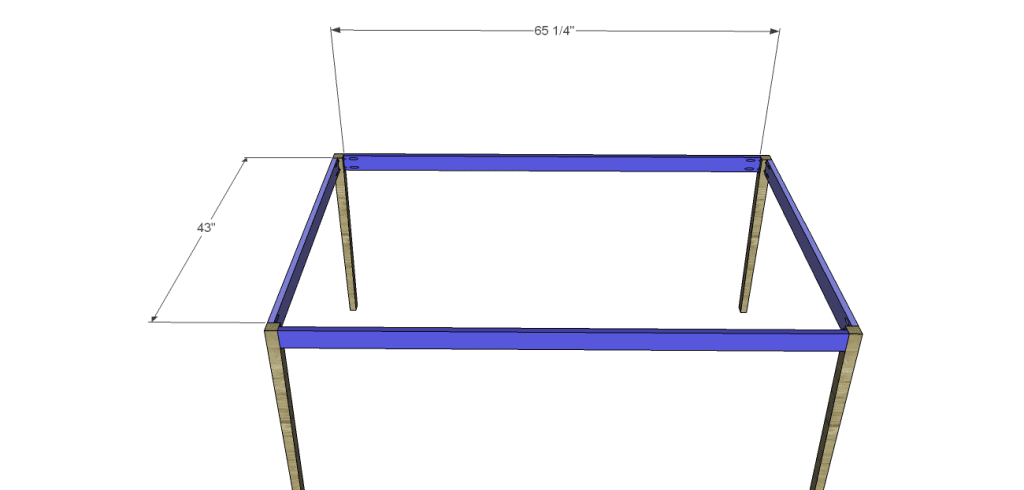
• 2 – 1×3 at 65-1/4″ – Aprons
• 2 – 1×3 at 43″ – Aprons
• 2 – 1×3 at 66-3/4″ – Top Supports
• 2 – 1×3 at 11-3/8″ – Stretchers
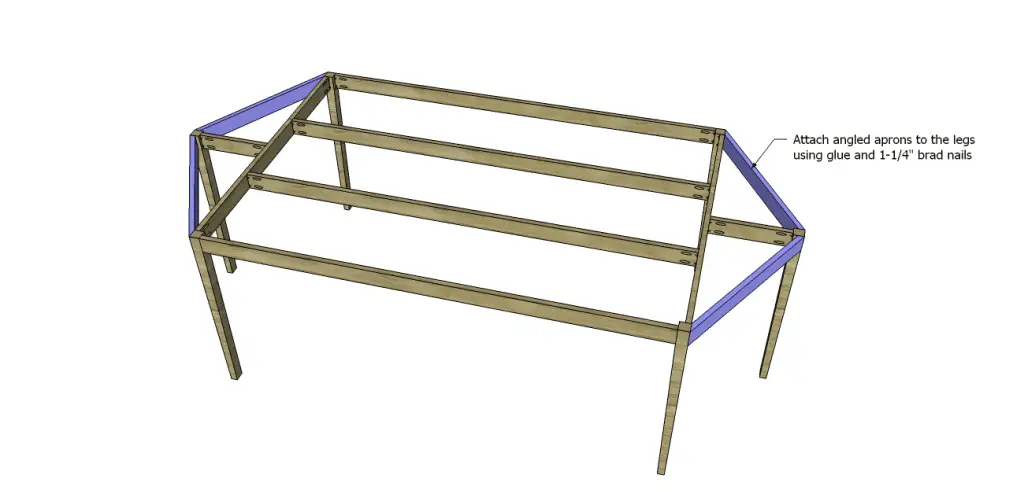
• 4 – 1×3 at 25-3/4″ – Angled Aprons
• 1 – 3/4″ plywood at 48″ x 96″ – Top

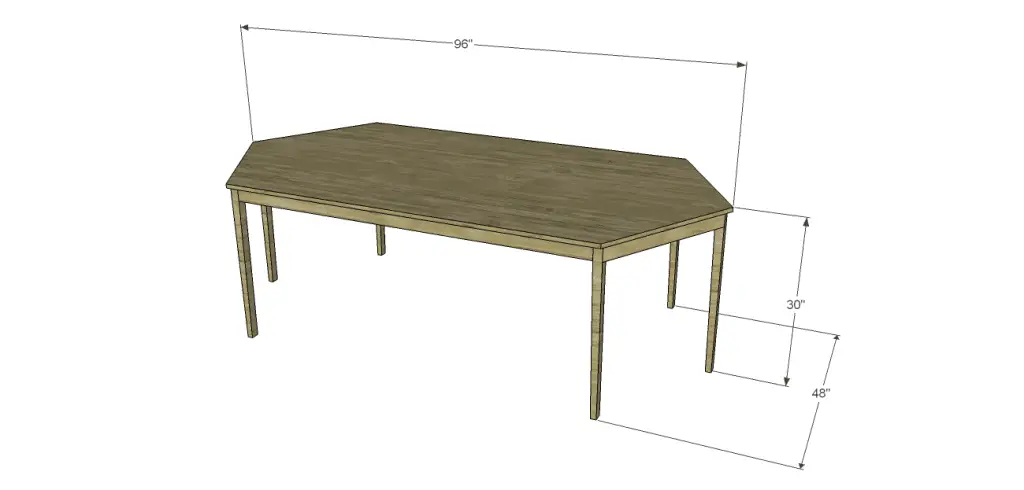
Notes:

Edge banding will be applied to the exposed edges of the plywood prior to assembly.

 

Step One

Cut the pieces for the legs. Cut the taper using a jigsaw, bandsaw, or tapering jig on the table saw.

 

Step Two

Cut the pieces for the aprons. With the pocket hole jig set for 3/4″ material, drill pocket holes in each end of the apron pieces. Assemble the table frame as shown – the tapers of the legs will face each other at the shorter sides – using glue and 1-1/4″ pocket hole screws. The outside face of each apron will be flush with the outside face of the legs.

 

Step Three

Cut the pieces for the center supports and drill pocket holes at each end. Secure to the longer stretchers using glue and 1-1/4″ pocket hole screws.

 

Step Four

Cut the pieces for the stretchers and drill pocket holes at each end. Secure the stretchers to the outside of the longer aprons as well as the two remaining legs using glue and 1-1/4″ pocket hole screws. The taper for the legs will face in toward the long stretchers.

 

Step Five

Cut the pieces for the angled aprons. I have given the measurement as well as the degree for each angle. When attaching to the table frame, the 30 degree angled side will attach to the leg with the short stretcher and the 60 degree angled side will attach to the corner leg. Attach the aprons with glue and 1-1/4″ brad nails.

 

Step Six

Cut the piece for the top. Spread glue along the top supports, the aprons, the stretchers, and the legs and position the top so that it overhangs by 1″ on all sides. Secure to the frame using glue and 1-1/4″ brad nails.

 

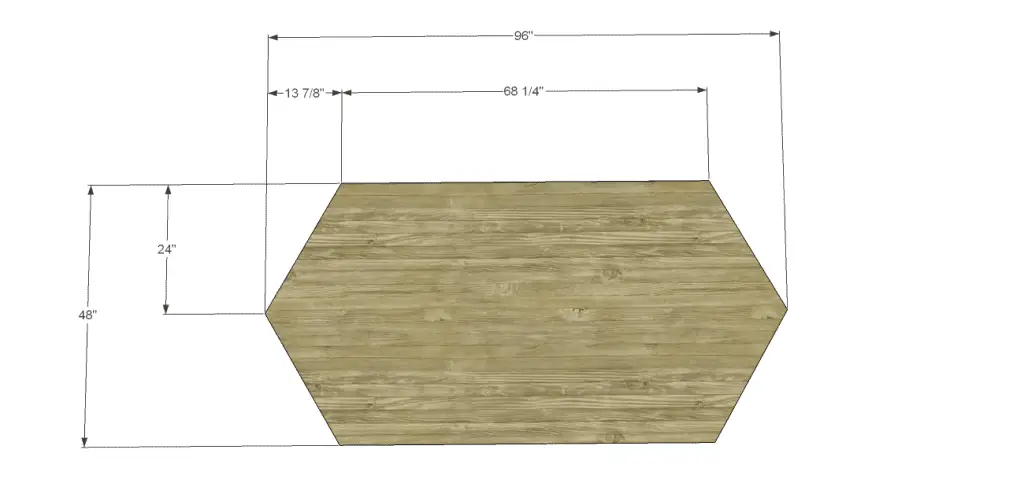
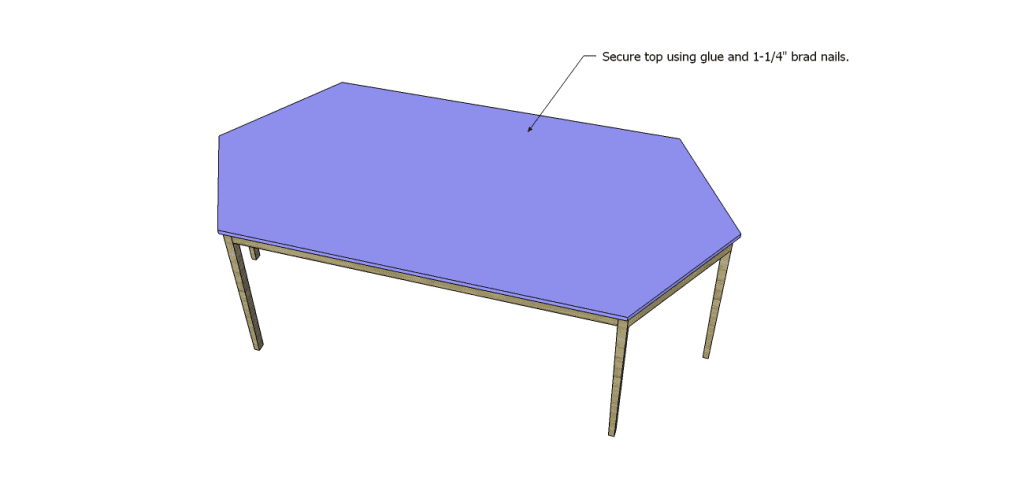
Finish as desired!

I love these free furniture plans to build an Elongated Hexagon Table. It is a great choice for those new to woodworking! Do you have a request for plans? Contact me at cher {at} designsbystudioc {dot} com!

Disclaimer:

This post contains links to a site of which I am an affiliate. What that means is if the link is clicked and a purchase is made, I will get a commission of that sale. Rest assured I would only direct my readers to sites I shop at myself!

Originally posted 2014-01-17 08:00:34.